Matematica in pillole: la successione di Fibonacci

Avete mai sentito parlare della successione numerica di Fibonacci? Sapevate che se ne trovano esempi anche in natura?

In questo articolo, tratto da Compiti a casa. Come aiutare tuo figlio in matematica di Carol Vorderman, conosceremo la successione di Fibonacci, impareremo a disegnare una spirale e vedremo come anche la natura rispetti questa regola matematica:

• Cos'è la successione di Fibonacci
• Come disegnare una spirale di Fibonacci
• Fibonacci in natura

Cos'è la successione di Fibonacci

Una successione numerica è una serie di numeri scritti sotto forma di lista che segue un andamento, o “regola”, particolare. Ogni numero in una successione viene chiamato “termine”. Il valore di ogni termine in una successione può essere individuato utilizzando le regole specifiche di quella data successione. 
Alcune successioni seguono delle regole che sono leggermente più complesse, ma che tuttavia possono essere molto significative. Due esempi di queste regole sono i numeri al quadrato e la successione di Fibonacci, detta anche successione aurea.

La successione di Fibonacci è una successione molto famosa, che appare spesso in natura e in architettura. I primi due termini sono entrambi 1, poi ogni termine è la somma dei due termini che lo precedono.

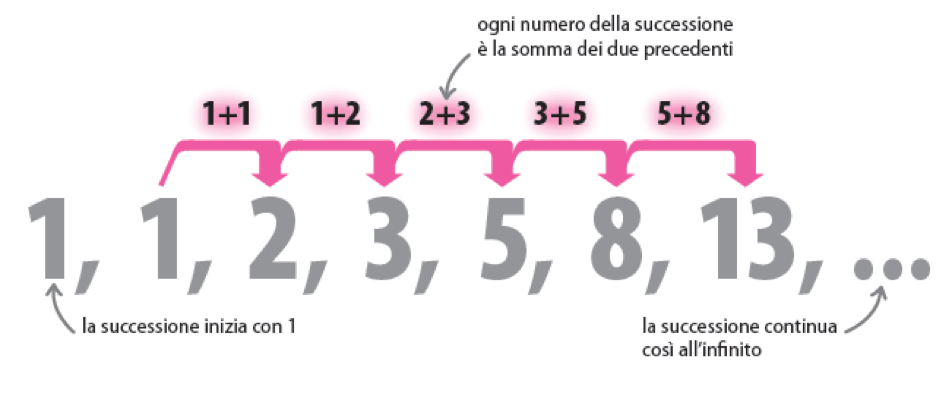
Come disegnare una spirale di Fibonacci

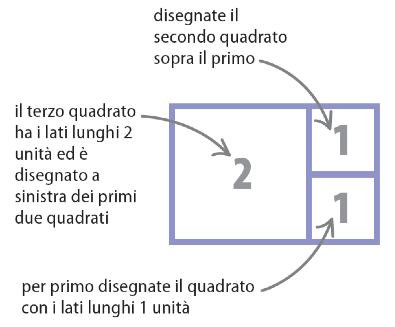
Utilizzando i numeri nella successione di Fibonacci si può disegnare una spirale, tracciando prima dei quadrati con i lati lunghi quanto ogni termine della sequenza, poi disegnando delle curve che toccano gli angoli opposti dei quadrati.

1. Per primo disegnate il quadrato con i lati di 1 unità sia in lunghezza che in altezza. Disegnatene un altro identico sopra, poi disegnate un quadrato con i lati di 2 unità vicino a quelli di 1 unità. Ogni quadrato rappresenta un termine della sequenza.
   
   
   
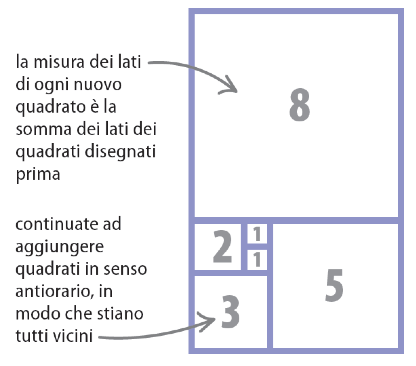
2. Continuate ad aggiungere quadrati che rappresentano i termini della sequenza di Fibonacci, aggiungendoli in senso antiorario. Questa immagine mostra i primi sei termini della sequenza.
   
   
   
   
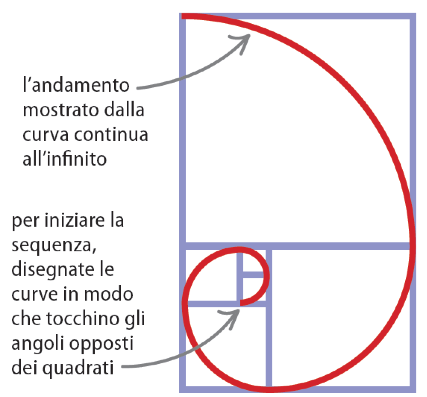
3. Infine disegnate le curve in modo che tocchino gli angoli opposti dei quadrati, iniziando dal centro e continuando verso l’esterno in senso antiorario. Questa curva viene chiamata spirale di Fibonacci.
   
   

Fibonacci in natura

Le prove della successione di Fibonacci possono riscontrarsi ovunque, anche in natura. La successione forma una spirale e si può osservare nella spirale di una conchiglia o nella disposizione dei semi in un girasole. Questa forma prende il nome da Leonardo Fibonacci, un matematico italiano.